Locked Candidates Type 1 (Pointing)
If in a box all the candidates of a specific digit are confined to only one row or column, that digit cannot appear outside of that box in the same row or column.
Let's have a look at an example to understand Locked Candidates a little better.
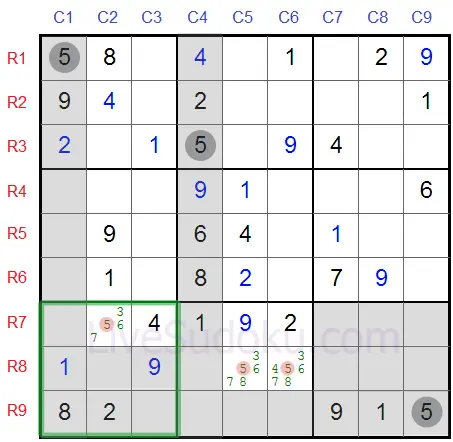
Have a look at this Sudoku.
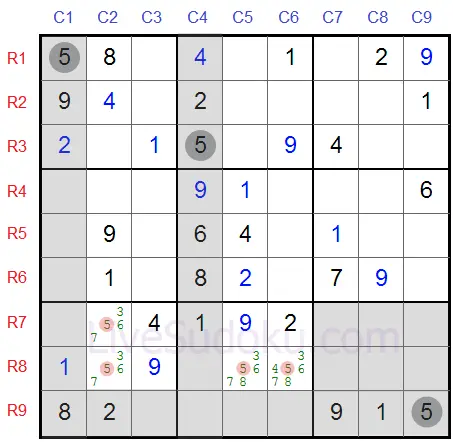
We are looking for the possible cells for '5' in the lower boxes, they are marked in red.
Now look at the mid-lower box in particular - this box has to contain '5'
It has to be on either R8C5 or R8C6 and these cells are on the same row - row #8.
This means that on row #8 no cells other than these two can contain the digit 5.
A digit can appear only once on every row - and we've already established that either R8C5 or R8C6 must be '5'.
So we can eliminate 5 from all other cells in this row, in particular R8C2.
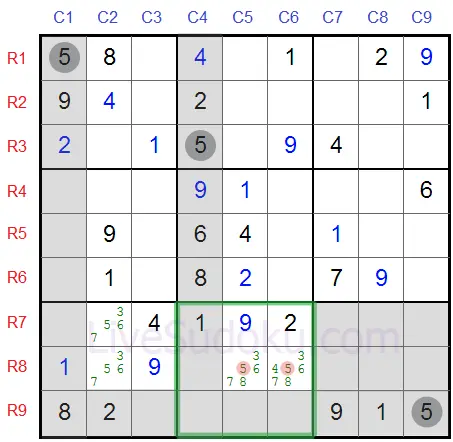
Now take a look at the box #7 (marked on the grid).
There is only one candidate left for '5' - R7C2 - it is a Hidden Single and must contain '5'.
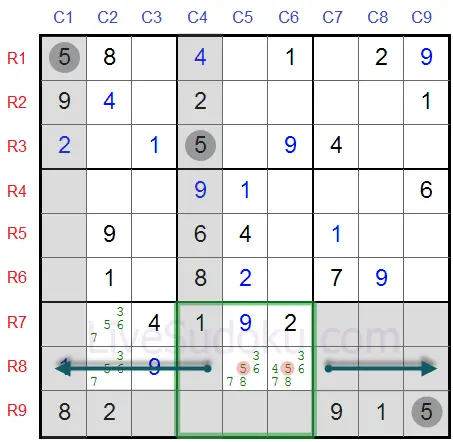
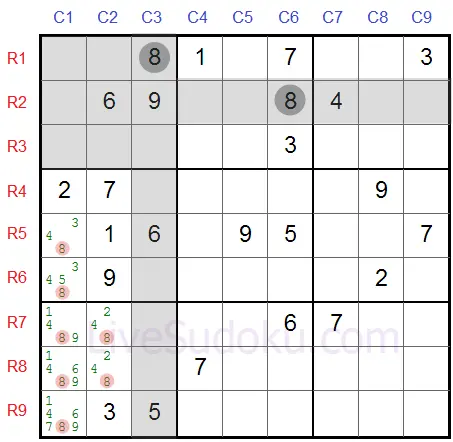
Let's have a look at another example, can you see the locked candidate in this sample?
Hint: it's in a column this time.
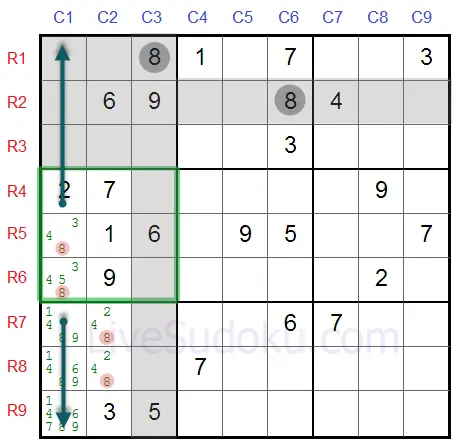
In the mid-left box, '8' has to be on R5C1 or R6C1 - which are both on the same column #1.
This means that on column #1 - no cells other than these two can contain the digit '8' - a digit can appear once on every column and we established that R5C1 or R6C1 must be '8'.
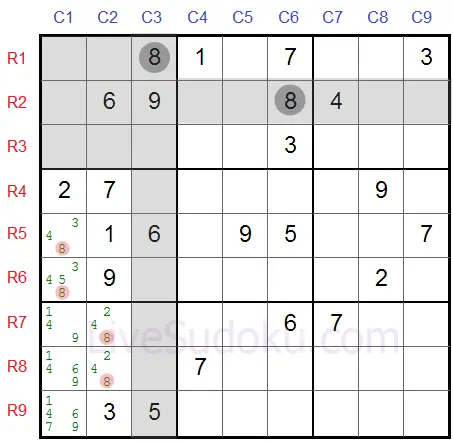
So we can eliminate '8' from all other cells in this row - R7C1, R8C1 and R9C1.
Some moves such as this one are helping eliminate candidates from cells - and not necessarily solve the cells - which will be achieved through additional moves and methods.