Have a look at this Sudoku. We are looking for the possible cells for 5 in the lower boxes; they are marked in red.
Box 8 must contain a 5, and its only options are R8C5 and R8C6. Both sit on row 8.
Since one of those two cells must be 5, no other cell on row 8 can contain 5. In particular, we can eliminate 5 from R8C2.
Now look at box 7: only one candidate for 5 remains, R7C2. It is a hidden single and must be 5.
Look at this sample and try to find the locked candidate. Hint: it is in a column this time.
In box 4, 8 must sit at R5C1 or R6C1, both in column 1.
So 8 can be removed from all other cells in column 1: R7C1, R8C1, and R9C1.
Moves like this one eliminate candidates rather than solve cells; the solved cells come from the follow-up moves.
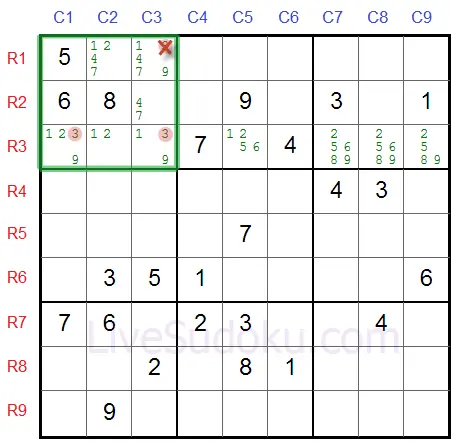
Look at row 3, with pencil marks filled for the whole row. The row must contain a 3, and its only possible cells are R3C1 and R3C3. Both are in box 1.
Because one of those two cells must be 3, no other cell in box 1 can contain 3. Every other candidate 3 in the box can be removed.
Here is the same idea in a column. Column 1 must contain a 1, and its only options are R7C1 and R8C1. Both are in box 7.
Since either R7C1 or R8C1 will be 1, we can safely eliminate 1 from all other cells in box 7.
Highlight one digit and read the grid: where can it still go in each box? The pattern jumps out without writing a single pencil mark.
If a digit is confined to a specific row or column within a box, like row 8 here, that digit is blocked from the rest of the row or column.
Lesson complete
Nice work - you went through every step. Ready for the next lesson?
Next: Naked Pairs and Triples in SudokuWhat locked candidates are
Locked candidates is an elimination technique for situations where all remaining positions for a digit are trapped in the overlap of a box and a line. It comes in two directions: pointing (Type 1), where a box locks a digit onto one row or column, and claiming (Type 2), where a row or column locks a digit into one box.
Either way, the digit can be removed from the rest of the affected house. Locked candidates does not solve a cell directly, but it regularly uncovers new singles.
Pointing (Type 1): a box locks a row or column
If all candidates for a digit inside a box sit on a single row or column, that digit cannot appear elsewhere on the same row or column outside the box.
Pointing in a column
The same pattern happens vertically. When the candidates of a digit inside a box share one column, the digit is blocked from that column outside the box.
Claiming (Type 2): a line locks a box
Claiming is the mirror image of pointing. If all candidates for a digit in a row or column fall inside a single box, the digit can be eliminated from the other cells of that box.
How to find locked candidates
Whenever a digit's candidates are confined to one row or column within a box, you have a potential locked candidate. You do not need full pencil marks to spot them.
Walk through this in steps 12-13 of the guided example above
Frequently asked questions
What is the difference between pointing and claiming?
Pointing goes from box to line: a box locks a digit onto one row or column. Claiming goes from line to box: a row or column locks a digit into one box. The elimination direction is opposite.
Does locked candidates solve a cell?
Not directly. It removes candidates, and the removals frequently create hidden or naked singles nearby.
When should I look for locked candidates?
As soon as singles stop appearing. It is the easiest elimination technique and the natural first step beyond beginner moves.
Practice next
Locked candidates start appearing in medium and hard puzzles. Highlight one digit at a time and scan each box for confined candidates.