Candidatos Bloqueados Tipo 1 (Apontando)
Se, em uma caixa, todos os candidatos de um número em específico estão confinados a apenas uma coluna ou linha, aquele número não pode aparecer fora daquela caixa na mesma linha ou coluna.
Vamos dar uma olhada em um exemplo para você entender melhor.
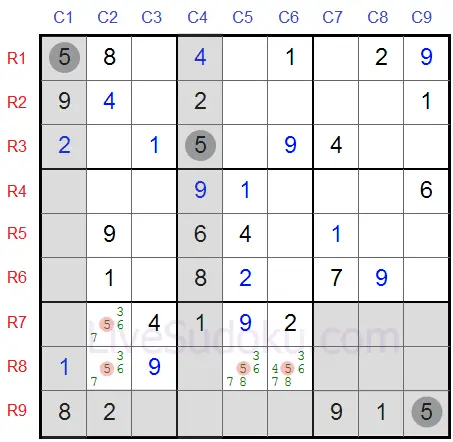
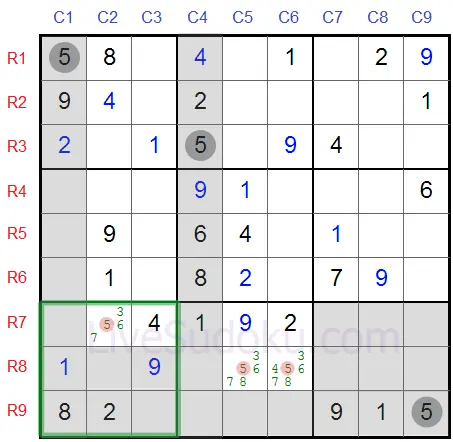
Dê uma olhada neste Sudoku.
Nós estamos olhando para as possíveis células para '5' nas caixas inferiores, destacadas em vermelho.
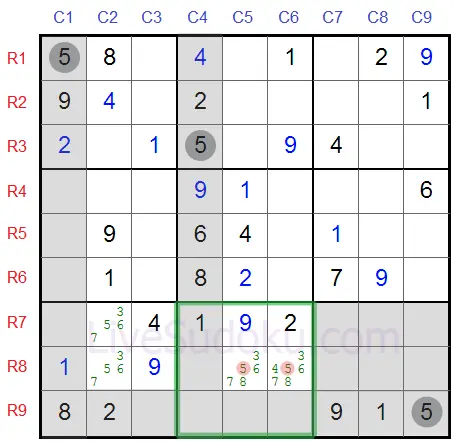
Agora, veja a caixa inferior-central em particular - esta caixa precisa de um '5'
Ele precisa aparecer em R8C5 ou R8C6, e estas células estão na mesma linha - linha #8.
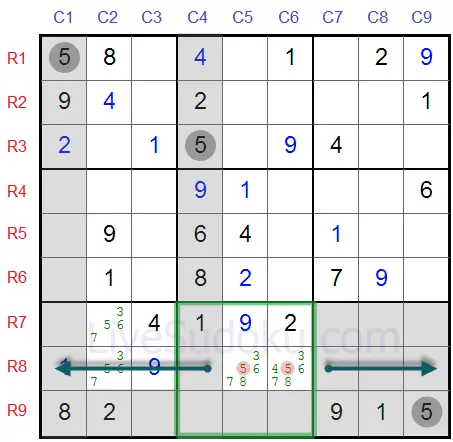
Isso significa que na linha #8, nenhuma das células que não sejam estas duas, podem conter o número 5.
Um número pode aparecer pelo menos uma vez em cada linha, e já estabelecemos que R8C5 ou R8C6 precisam ser '5'.
Então, podemos eliminar o número 5 de todas as outras células nesta linha, em particular R8C2.
Agora dê uma olhada na caixa #7 (destacada na grade).
Há apenas um candidato sobrando para '5' - R7C2 - é um número Solitário Oculto e precisa ser '5'.
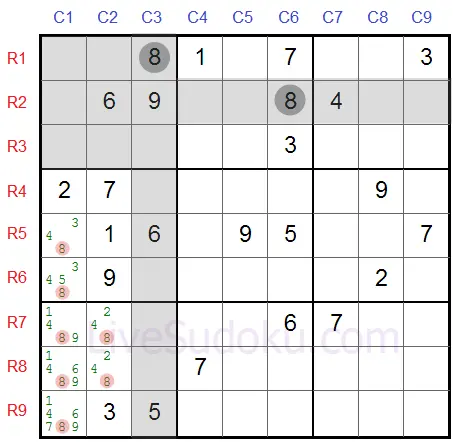
Vamos dar uma olhada em outro exemplo, você consegue identificar o candidato bloqueado?
Dica: ele está na coluna.
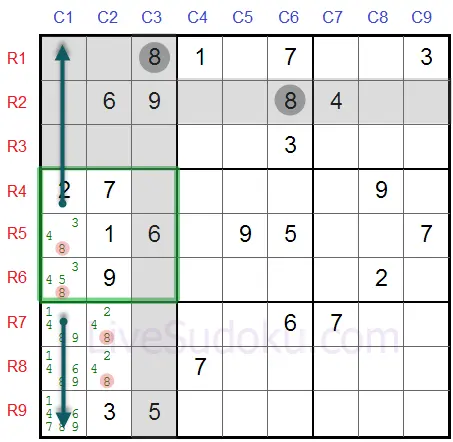
Na caixa central-esquerda, '8' precisa estar em R5C1 ou R6C1 - e ambos estão na coluna #1.
Isso significa que nenhuma outra célula além destas duas podem ter o número '8' na coluna #1 - um número pode aparecer apenas uma vez por coluna e estabelecemos que R5C1 ou R6C1 precisam ser '8'.
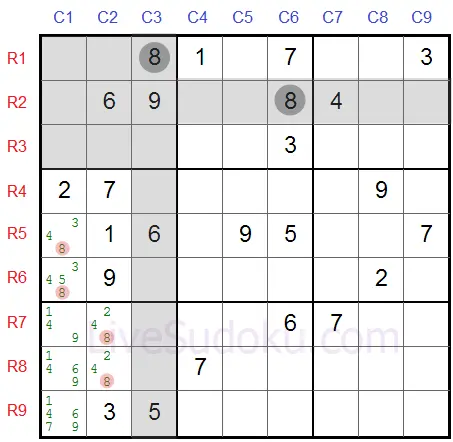
Então, podemos eliminar '8' de todas as outras células nessa coluna - R7C1, R8C1 e R9C1.
Alguns movimentos como este ajudam a eliminar candidatos de algumas células - mas não necessariamente resolvem tais células - que será alcançado através de movimentos e métodos adicionais.