Singletons nus
Vous vous souvenez des cellules compagnons?
Les cellules compagnons sont des cellules qui sont dans la même maison (même ligne, même colonne ou même case).
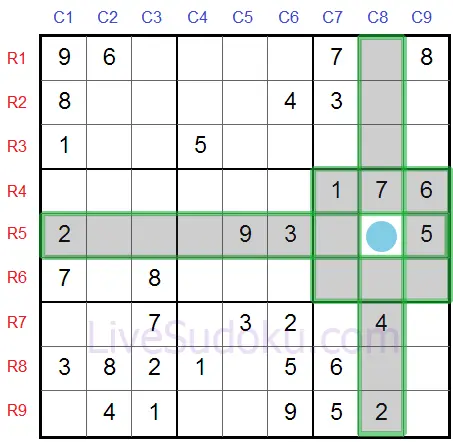
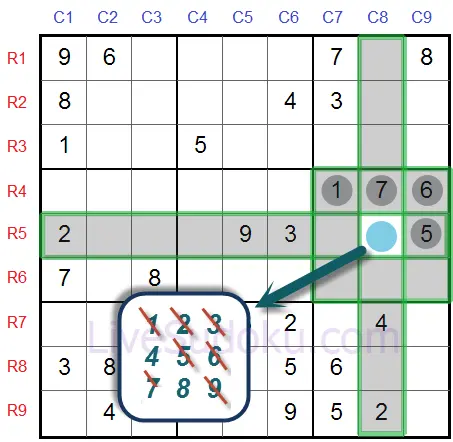
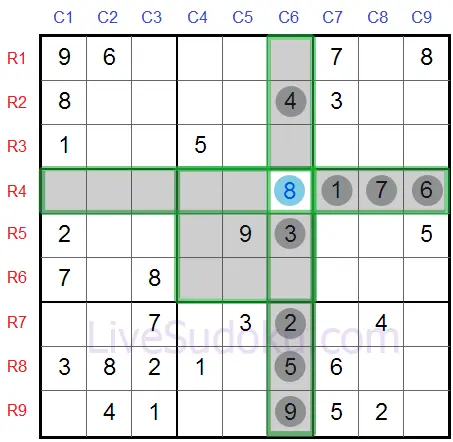
Regardez R5C8 dans ce puzzle, ses cellules compagnons sont surlignées en gris.
Examinons les valeurs possibles de R5C8 - ce sont des candidats.
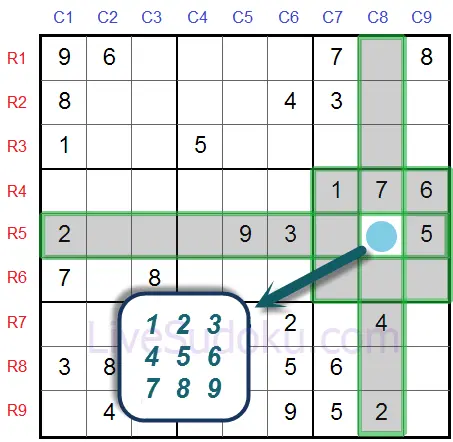
Pour commencer, R5C8 peut être n'importe quel chiffre entre '1' et '9'.
Alors gardons une note de cela sur le côté.
Les notes dans l'image sont appelées marques stylo et nous en discuterons plus en détail dans le prochain tutoriel
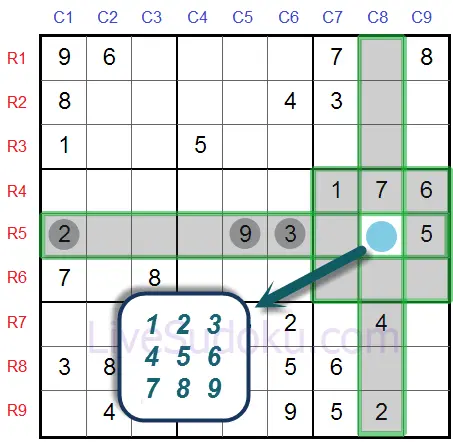
En regardant la ligne numéro 5 - nous avons déjà '2', '9'et '3' déjà utilisés.
Étant sur la même ligne que R5C8, cela signifie que R5C8 ne peut pas contenir '2', '3' ou '9'.
La règle basique dit qu'un chiffre ne peut apparaître qu'une seule fois sur la même ligne.
Supprimons donc '2', '3' et '9' de notre liste de candidats.
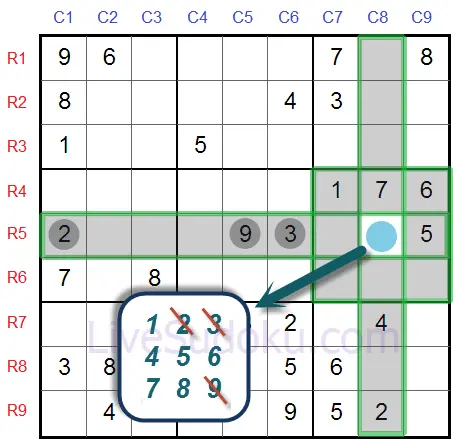
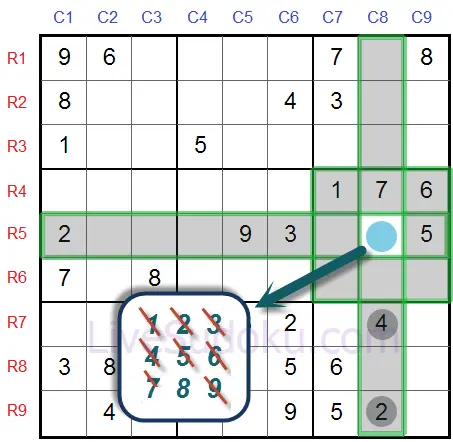
En regardant le cas de R5C8 - nous avons déjà utilisé '1', '5', '6', et '7'.
La règle basique dit qu'un chiffre ne peut apparaître qu'une seule fois sur la même case,
Eliminons donc '1', '5', '6' et '7' de notre liste de candidats pour R5C8.
Enfin, nous allons examiner la colonne de R5C8 - elle a '2' et '4'.
Une fois de plus, un chiffre ne peut apparaître qu'une seule fois sur la même ligne, nous allons donc éliminer '2' et '4' de la liste des candidats pour R5 C8 ('2' a déjà été éliminé).
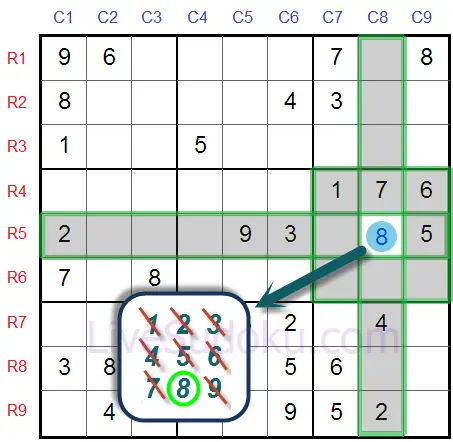
Ça y est, que nous reste-t-il sur notre liste de candidats pour R5C8?
Il n'y a qu'une seule possibilité et c'est un '8'.
Donc R5C8 doit être un '8'.
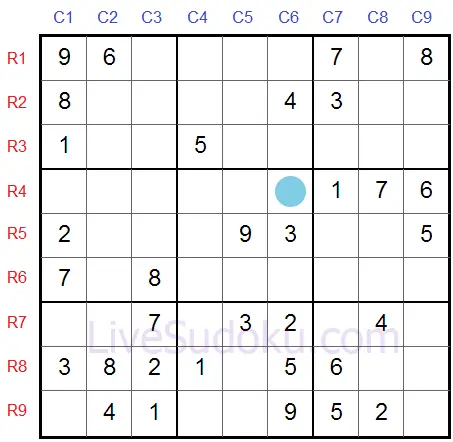
Voici un autre exemple de singleton nu.
Pouvez-vous deviner la réponse pour R4C6?
Encore une fois, c'est un '8', car ses cellules de contacts contiennent tous les chiffres de '1' à '9', à l'exception de '8'.