Naked Triple/ Triplets
If there are three cells in a house (row, column or box) that have the same 3 candidates, you can eliminate these 3 candidates from all the other cells in that house.
Not all 3 cells must contain all 3 candidates, but these 3 cells should contain the 3 candidates between them and not more than 3 candidates in each cell.
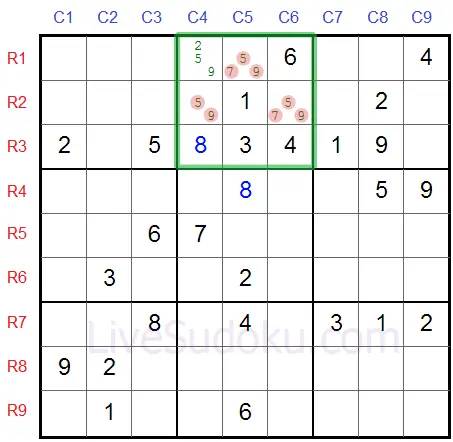
Check out R3C5, R2C4 and R2C6 in the box below.
These 3 cells candidates are '5', '7' and/or '9'.
It is certain that these 3 cells will be '5', '7' or '9'. It's still unknown which is which, but it doesn't matter. These 3 cells have no other option.
This means that no other cells in this box can be '5', '7' or '9'
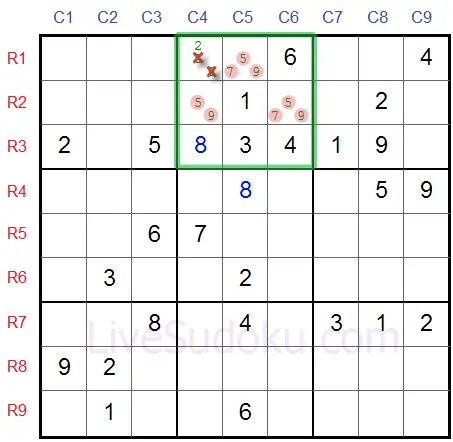
We can eliminate '5' and '9' from R1C4 and we find out that R1C4 has only candidate so we can solve it.
Here is another interesting example of a triplet in a box.
The 3 marked cells only have 2 candidates each, but together they do form a triplet.
The candidates '1', '3' and '7' are spread over 3 cells and therefore one cell has to be a '1', the other a '3' and the other a '7'.
No other cells can be '1', '3' or '7', so we can eliminate them from all other cells.